DIOPHANTE D’ALEXANDRIE

DIOPHANTE D’ALEXANDRIE

De la vie de Diophante, nous ne connaissons presque rien: Alexandrin, il vécut après Hypsiclès et avant Théon d’Alexandrie, c’est-à-dire après la première moitié du II^e siècle avant notre ère, et avant la seconde moitié du IV^e siècle de notre ère. Nos certitudes s’arrêtent là, pour céder la place à de simples conjectures. Deux témoignages tardifs tentent en effet de préciser davantage les dates de Diophante. Le premier revient à Michel Psellus (1020-1105?) dont, au XIX^e siècle, l’historien des sciences Paul Tannery a restitué et commenté un fragment, pour conclure que Diophante aurait été l’ami d’un certain Anatolius, lequel a été identifié – toujours par Tannery – comme Anatolius d’Alexandrie; il s’agit de celui qui devint en 270 évêque de Laodicée (Syrie), que l’historien Eusèbe de Césarée loue pour ses connaissances scientifiques, et dont le mathématicien Jamblique a conservé certains fragments des travaux arithmétiques. Poussant plus loin sa conjecture, Tannery, non sans audace, fait de Diophante un mathématicien chrétien directement disciple de Denys, évêque d’Alexandrie de 248 à 265.

La plupart des historiens de la science hellène, comme Friedrich Otto Hultsch et Thomas Heath, n’ont pas retenu cette conjecture. L’autre témoignage est celui du bio-bibliographe du XIII^e siècle, Ab al-Faraj, qui affirme sans donner ses sources que Diophante vivait sous le règne de Julien l’Apostat (361-363). Mais il peut s’agir là d’une confusion entre le mathématicien et un rhéteur du même nom.

À défaut de nouveaux arguments décisifs, nous nous contenterons, pour l’heure, d’admettre qu’il s’agit d’un Alexandrin, dont la vie s’écoula probablement entre le deuxième et le troisième siècle et dura, si l’on en croit un célèbre épigramme de l’Anthologie palatine attribué à Métrodore de Byzance (IV^e siècle), quatre-vingt-quatre ans.

1. Une œuvre dispersée

De l’œuvre mathématique attribuée à Diophante, la tradition manuscrite grecque nous a transmis six livres d’un ouvrage sur les Problèmes arithmétiques , et, d’autre part, un chapitre d’un livre sur les Nombres polygones. Les Arithmétiques , qui ont assuré à Diophante son grand destin historique, devaient comprendre treize livres, selon les termes mêmes de l’auteur au préambule du premier livre. Mais, comme seuls six livres avaient été conservés en grec, les historiens, depuis le XIX^e siècle – G. H. F. Nesselmann, Henry Thomas Colebrooke, Hermann Hankel, Paul Tannery, Charles Henry, Thomas Heath et d’autres – ont avancé plusieurs hypothèses pour tenter d’expliquer la perte des sept autres livres, voire parfois pour essayer de définir leur contenu.

Or, on savait, par les bio-bibliographes arabes du X^e siècle, qu’il existait une traduction arabe des Arithmétiques , par Qus レ ibn L q de Baalbek, et datant de la seconde moitié du IX^e siècle. Au XIX^e siècle, l’historien des sciences Franz Woepcke a remarqué que al-Karaj 稜, mathématicien arabe de la fin du X^e siècle, a résumé les trois premiers livres de cette traduction qui, globalement, correspondent aux trois premiers livres du texte grec tel qu’il nous est parvenu. En 1971, Roshdi Rashed a pu retrouver à Meshed, en Iran, quatre livres de la traduction arabe, tous perdus en grec, et il a établi qu’ils suivent, dans l’ordre, les trois premiers livres du texte grec. Cette découverte a ruiné toutes les interprétations évoquées plus haut.

2. Les «Arithmétiques»

Telles qu’elles se présentent maintenant, les Arithmétiques comprennent au moins dix livres, dans l’ordre suivant: les trois premiers livres grecs, immédiatement suivis, et dans l’ordre, par les quatre livres retrouvés de la version arabe. Viennent ensuite les livres IV et V du texte grec, dont l’organisation appelle un examen approfondi, en cours, et enfin, le livre VI du texte grec, sur les triangles rectangles numériques.

Ainsi, des treize livres qu’aux dires de Diophante comportaient les Arithmétiques , nous en possédons actuellement au moins dix, et non plus seulement six. Et les livres retrouvés dans leur version arabe ne modifient pas seulement l’organisation des Arithmétiques , mais aussi leur extension ainsi que leur compréhension.

L’objet des «Arithmétiques»

Quel est, au juste, l’objet de Diophante dans les Arithmétiques ? Les réponses à cette question se présentent comme un conflit d’interprétations, dont les origines remontent déjà aux mathématiciens arabes du X^e siècle; de la logistique théorique à la géométrie algébrique, le spectre de l’interprétation de l’œuvre du mathématicien alexandrin est singulièrement étendu. Alors que Tannery hier, Kurt Vogel aujourd’hui voient dans les Arithmétiques une logistique théorique, Nesselmann, Hankel, Heath, naguère, et bien d’autres encore aujourd’hui soutiennent que l’on y trouve bien de l’algèbre. Des mathématiciens contemporains, tels André Weil, Jean Dieudonné, Isabelle G. Bašmakova, croient pouvoir, quant à eux, lire dans les Arithmétiques , sinon en toutes lettres, du moins en filigrane, les concepts et les instruments de la géométrie algébrique; dans ce cas Diophante ne serait pas seulement le prédécesseur de Fermat, mais de Hilbert, de Hurwitz et de Poincaré, et serait alors l’ancêtre de tous ces chapitres qui portent aujourd’hui son nom – analyse diophantienne, géométrie diophantienne, approximations diophantiennes, équations diophantiennes.

Organisation et nature des «Arithmétiques»

Mais, avant de confronter ces interprétations, décrivons les Arithmétiques. Le but de Diophante y est clair: édifier une théorie mathématique dont les éléments constitutifs seraient les nombres, considérés comme pluralités d’unités, et les parties fractionnaires comme fractions de grandeurs. Ces éléments de la théorie ne sont pas seulement présents «en personne», mais aussi comme espèces des nombres. On peut montrer que cette expression, «espèce» de nombre, recouvre également et indifféremment la puissance d’une pluralité déterminée, et la puissance d’une pluralité quelconque, c’est-à-dire provisoirement indéterminée, mais qui sera, à la fin de la solution du problème, toujours déterminée: il s’agit du nombre «non dit», 見凞礼塚礼﨟 見福晴猪礼﨟. Dans le préambule du premier livre, Diophante définit ces termes, ces puissances, jusqu’à la sixième, et en donne certaines abréviations (et non pas, comme on l’a toujours affirmé, une représentation symbolique). Au quatrième livre – selon le nouvel ordre – il définit la huitième et la neuvième puissance. Notons que la septième puissance n’est jamais mentionnée par Diophante, et que la cinquième n’apparaît jamais dans les énoncés des problèmes des Arithmétiques . Cela nous ramène à cette notion, déjà évoquée, d’«espèce» de nombre. Il faut en effet rappeler que Diophante parle de trois espèces: celle du nombre linéaire, celle du nombre plan, et enfin celle du nombre solide. C’est seulement à propos de ces trois espèces qu’il parle de la nature ( 﨏羽靖晴﨟) des nombres. Ces espèces engendrent toutes les autres, lesquelles doivent, à la limite, prendre leurs noms. Ainsi, le carré-carré, 嗀羽益見猪礼嗀羽益見猪晴﨟, noté ^Y , est un carré – 嗀羽益見猪晴﨟 – ^Y; le carré-carré-carré, le carré-cubo-cube sont également des carrés; le cubo-cubo-cube est un cube. Autrement dit, les espèces engendrées ne peuvent l’être que par composition , et la puissance de chacune est nécessairement un multiple de 2 ou de 3. On comprend alors pourquoi la septième puissance est absente, et pourquoi la cinquième n’apparaît pas dans les énoncés. On sait également quelle est l’importance de cet aspect, tant pour la formulation des problèmes que pour leur résolution.

La composition des Arithmétiques s’éclaire du même coup: il s’agit de combiner ces espèces entre elles, sous certaines contraintes et à l’aide des opérations de l’arithmétique élémentaire; résoudre les problèmes, c’est essayer de poursuivre dans chaque cas «jusqu’à ce qu’il reste une seule espèce de part et d’autre».

Mais si l’on examine systématiquement le texte de Diophante, on constate que, par «solution», l’auteur entend des nombres déterminés, autrement dit des rationnels positifs. Il arrive même qu’avant d’entreprendre la discussion, il impose aux nombres donnés et aux paramètres des conditions supplémentaires telles que le problème admette une seule solution rationnelle. Le problème est alors qualifié de 神凞見靖猪見精晴礼﨟, «convenablement déterminé». Une telle conception de la solution explique pourquoi à aucun moment Diophante ne distingue entre problèmes déterminés et problèmes indéterminés, et pourquoi ne figure nulle part l’examen des problèmes impossibles comme tel. On constate en effet que, dans les Arithmétiques , des problèmes déterminés s’intercalent entre les problèmes indéterminés; on remarque également que des problèmes qui avaient leur place dans cet ouvrage en sont absents, tel celui de la somme de deux cubes égale à un cube.

Si donc Diophante procède, au cours de ses solutions, par substitution, élimination et déplacement des espèces, bref, à l’aide de techniques algébriques, les Arithmétiques ne sont cependant pas un traité d’algèbre. Il s’agit bien, en effet, d’un livre d’arithmétique, non pas dans l’anneau des entiers relatifs, mais dans le demi-corps des rationnels positifs; et c’est au cadre relativement étroit de ce demi-corps que, semble-t-il, il faut imputer la principale responsabilité du développement des techniques algébriques, qui furent sans aucun doute d’un précieux secours aux algébristes arabes.

Dans les mathématiques hellénistiques, nous ne connaissons aucune influence des Arithmétiques. Un passage du Lexique de Suidas a fait bien des ravages en attribuant à Hypatie un commentaire du Canon astronomique de Diophante. Mais on sait depuis Fabricius qu’il s’agit en fait d’un passage altéré, qu’il convient plutôt d’attribuer à Ptolémée. Avec beaucoup de témérité, Tannery a modifié le texte pour attribuer à Hypatie un commentaire de Diophante, suscitant ainsi une légende. Or, il a en fait fallu attendre les mathématiciens arabes, et les commencements de l’algèbre par al-Khw rizm 稜 et ses successeurs, pour que les Arithmétiques fussent lues et commentées; mais, pour la plupart, ces commentaires les ont infléchies dans un sens algébrique, pour qu’elles trouvent enfin leur place au nombre des travaux sur l’analyse indéterminée; elles communiquèrent d’ailleurs une notable impulsion au développement de ce chapitre, qui fut alors désigné par un titre propre: f 稜 al-’istiqr ’ – l’analyse indéterminée –, ainsi qu’en témoignent les travaux d’al-Karaj 稜 et de ses successeurs. Or, cette interprétation algébrique qui, selon nous, ne traduit pas le sens profond de l’œuvre de Diophante, a survécu aux mathématiciens arabes, puisqu’on la retrouve chez les algébristes du XVI^e siècle comme Raffaele Bombelli et Simon Stevin, entre autres, et même d’ailleurs chez bien des historiens des mathématiques. Les tenants de cette interprétation s’accordent, par-delà leurs divergences, pour voir dans les livres de Diophante une succession de problèmes équivalents, dans leur grande majorité, à des équations (ou à des systèmes d’équations) indéterminées, de degré inférieur ou égal à 9, à deux ou plusieurs inconnues, et ne contenant que des quantités rationnelles; les solutions de ces équations doivent être des nombres rationnels positifs, entiers si possible, mais aucune exigence n’est formulée sur ce point. Les Arithmétiques ne traitent que des nombres rationnels positifs; à aucun moment elles ne considèrent les nombres irrationnels algébriques pour eux-mêmes, non plus, du reste, que le critère de rationalité en général. S’il arrive à Diophante d’examiner les conditions de rationalité, c’est seulement pour rechercher une solution rationnelle positive. C’est finalement en termes de variables, de puissances, de paramètres et de solutions générales que l’on interprète les Arithmétiques.

Ainsi, lorsque Diophante cherche à résoudre (2.8) «partager un carré donné en deux carrés», l’algébriste traduit immédiatement: problème indéterminé du second degré à deux variables, équivalent à l’équation:

et comme, au cours de sa solution, il assigne à la donnée a une valeur particulière, on y voit une représentation d’un paramètre quelconque pour les cas semblables. Mais cette lecture des Arithmétiques laisse entière une difficulté ainsi exprimée par Hankel: «Of more general comprehensive methods there is in our author no trace discoverable: every question requires a quite special method, which after will not serve even for the most closely allied problems. It is on that account difficult for a modern mathematician even after studying 100 diophantine solutions to solve the 101rst problem ...»

Une classe de problèmes

C’est bien l’unité même des Arithmétiques qui est en question. Or le langage de la géométrie algébrique nous permet de mieux saisir cette unité, en nous aidant à dégager les algorithmes arithmétiques que le mathématicien alexandrin avait pu utiliser, sans toutefois leur attribuer la signification géométrique qu’ils ont à présent, et sans en donner la démonstration. Cette interprétation à la lumière de la géométrie algébrique est suscitée, en partie au moins, par ce désir de restituer l’unité des Arithmétiques , lesquelles vont désormais se présenter comme l’étude des points rationnels des ensembles algébriques irréductibles définis sur Q, de courbes, de surfaces et d’hypersurfaces. Mais, si on se limite au seul cas des courbes, cette recherche est, en principe, menée par des méthodes distinctes selon le genre des courbes. Or, si la plupart des courbes étudiées dans les Arithmétiques sont de genre 0, il existe cependant dans les livres grecs, comme on le savait auparavant, des courbes de genre 1; bien plus, on rencontre deux courbes de genre 2, l’une dans les livres grecs, et l’autre dans la version arabe. Dans ce dernier cas, il s’agit du problème (6.18) qui se réécrit:

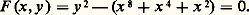Pour les courbes de genre 0, Diophante détermine les points rationnels par la méthode de la corde, sous différentes conditions qu’il serait difficile d’exposer ici. Prenons simplement l’exemple de l’équation (1). Le point (0, – a ) est un point simple du cercle défini par (1). Diophante coupe le cercle par une famille D (u ) de droites passant par ce point, soit:

Si on substitue dans (1), le résultant du cercle et de D (u ) s’écrit:

d’où:

L’application 淋 (u ) = [ 﨏 (u ), 祥 (u )] de la droite affine sur le cercle défini par (1) est birationnelle.

Diophante a également examiné la méthode de la corde pour les courbes de genre 1. Ainsi, par exemple, pour trouver un point de la courbe:

qui intervient dans le problème (6.17), il coupe par une famille de coniques d’équations:

et trouve le point (x = 1/4, y = 9/16), en faisant 﨡 = 1/2.

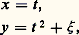Notons encore que Diophante utilise la méthode de la corde comme méthode d’élimination.

L’apport des Arithmétiques de Diophante à l’histoire des mathématiques dépasse les limites de ce chapitre sur l’analyse indéterminée constitué par les algébristes à partir du X^e siècle environ. La traduction arabe de l’ouvrage a, en effet, représenté, au même siècle, une contribution essentielle à la naissance de l’analyse diophantienne dans l’anneau des entiers relatifs, c’est-à-dire au sens où l’entendront plus tard Claude Gaspar Bachet de Méziriac et Fermat. Des mathématiciens du X^e siècle, comme al-Khujand 稜, al-Kh zin, ont en effet été conduits à l’analyse diophantienne entière, qui comportait l’étude de la théorie des triplets pythagoriciens, de la représentation des entiers comme somme de carrés, problème déjà abordé par Diophante. Ils ont également étudié des problèmes de congruences quadratiques, ont énoncé la conjecture de Fermat pour n = 3, et ont tenté d’en donner la démonstration. Ces études de la théorie des nombres ont été poursuivies plus tard par Bachet, Fermat et Euler. C’est au second que revient la conception de la «descente infinie» comme méthode de démonstration, rendant ainsi possible un nouvel essor de l’analyse diophantienne entière.

Encyclopédie Universelle. 2012.